解答・解説[1](2)
\(まず、円の中心と半径を求める。\)
\begin{eqnarray*}
x^2+y^2+2x-4y-4&=&0 を変形して\\
(x+1)^2-1+(y-2)^2-4-4&=&0\\
(x+1)^2+(y-2)^2&=&3^2\\
上の式より\\
中心(-1,2) 半径3\\
\end{eqnarray*}
\(l は、2x-y+k=0 と変形する。\)
\(円の中心をP、切り取られる線分の両端をA,Bとする。\)
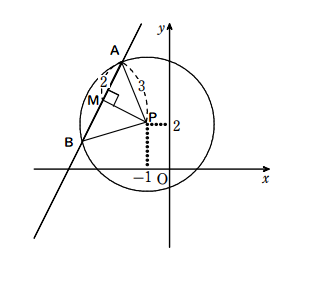
\(\Delta PABは、PA=PB=3 (円の半径)、AB=4 の二等辺三角形である。\\
ABの中点をMとすると、AM=BM=2、 PM \perp AMだから、\\
三平方の定理より、\)
\begin{eqnarray*}
PM^2&=&PA^2-AM^2 \\
&=&3^2-2^2 \\
&=&9-4 \\
&=&5 \\
PM&=&\sqrt{5} \\
\end{eqnarray*}
\(点と直線の距離の公式より\)
\begin{eqnarray*}
\frac{|2×(-1)+(-1)×2+k|}{\sqrt{2^2+(-1)^2}}&=&\sqrt5\\
\frac{|-2-2+k|}{\sqrt{5}}&=&\sqrt5\\
|-2-2+k|&=&5\\
-2-2+k&=&\pm 5\\
k&=&4\pm5\\
k&=&9,-1\\
\end{eqnarray*}
戻る
